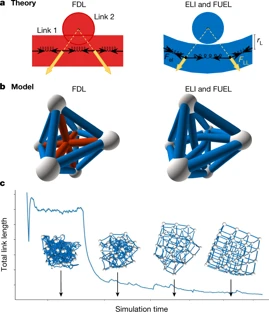
In many physical networks, including neurons in the brain three-dimensional integrated circuits and underground hyphal networks, the nodes and links are physical objects that cannot intersect or overlap with each other. To take this into account, non-crossing conditions can be imposed to constrain the geometry of networks, which consequently affects how they form, evolve and function. However, these constraints are not included in the theoretical frameworks that are currently used to characterize real networks. Most tools for laying out networks are variants of the force-directed layout algorithm—which assumes dimensionless nodes and links—and are therefore unable to reveal the geometry of densely packed physical networks. Here we develop a modelling framework that accounts for the physical sizes of nodes and links, allowing us to explore how non-crossing conditions affect the geometry of a network. For small link thicknesses, we observe a weakly interacting regime in which link crossings are avoided via local link rearrangements, without altering the overall geometry of the layout compared to the force-directed layout. Once the link thickness exceeds a threshold, a strongly interacting regime emerges in which multiple geometric quantities, such as the total link length and the link curvature, scale with the link thickness. We show that the crossover between the two regimes is driven by the non-crossing condition, which allows us to derive the transition point analytically and show that networks with large numbers of nodes will ultimately exist in the strongly interacting regime. We also find that networks in the weakly interacting regime display a solid-like response to stress, whereas in the strongly interacting regime they behave in a gel-like fashion. Networks in the weakly interacting regime are amenable to 3D printing and so can be used to visualize network geometry, and the strongly interacting regime provides insights into the scaling of the sizes of densely packed mammalian brains.

The concept of preferential attachment is behind the hubs and power laws seen in many networks. New results fuel an old debate about its origin, and beg the question of whether it is based on randomness or optimization.

Our focus is on networks capturing the collaboration between scientists and the calls between mobile phone users. We find that large groups persist for longer if they are capable of dynamically altering their membership, suggesting that an ability to change the group composition results in better adaptability. The behaviour of small groups displays the opposite tendency—the condition for stability is that their composition remains unchanged. We also show that knowledge of the time commitment of members to a given community can be used for estimating the community’s lifetime. These findings offer insight into the fundamental differences between the dynamics of small groups and large institutions.

The most highly connected proteins in the cell are the most important for its survival. Proteins are traditionally identified on the basis of their individual actions as catalysts, signalling molecules, or building blocks in cells and microorganisms. But our post-genomic view is expanding the protein’s role into an element in a network of protein–protein interactions as well, in which it has a contextual or cellular function within functional modules1,2. Here we provide quantitative support for this idea by demonstrating that the phenotypic consequence of a single gene deletion in the yeast Saccharomyces cerevisiae is affected to a large extent by the topological position of its protein product in the complex hierarchical web of molecular interactions.

Here we present a systematic comparative mathematical analysis of the metabolic networks of 43 organisms representing all three domains of life.We show that, despite significant variation in their individual constituents and pathways, these metabolic networks have the same topological scaling properties and show striking similarities to the inherent organization of complex non-biological systems. This may indicate that metabolic organization is not only identical for all living organisms, but also complies with the design principles of robust and error-tolerant scale-free networks, and may represent a common blueprint for the large-scale organization of interactions among all cellular constituents.

Here we demonstrate that error tolerance is not shared by all redundant systems: it is displayed only by a class of inhomogeneouslywired networks,called scale-free networks, which include theWorld-WideWeb, the Internet, social networks and cells. We find that such networks display an unexpected degree of robustness, the ability of their nodes to communicate being unaffected even by unrealistically high failure rates.However, error tolerance comes at a high price in that these networks are extremely vulnerable to attacks (that is, to the selection and removal of a few nodes that play a vital role in maintaining the network’s connectivity). Such error tolerance and attack vulnerability are generic properties of communication networks.

Despite its increasing role in communication, the World-Wide Web remains uncontrolled: any individual or institution can create a website with any number of documents and links. This unregulated growth leads to a huge and complex web, which becomes a large directed graph whose vertices are documents and whose edges are links (URLs) that point from one document to another. The topology of this graph determines the web’s connectivity and consequently how effectively we can locate information on it.